Операции над множествами

Множества в Python пришли из математики, где над ними можно совершать такие операции как объединение и пересечение, а также находить разность и симметричную разность.

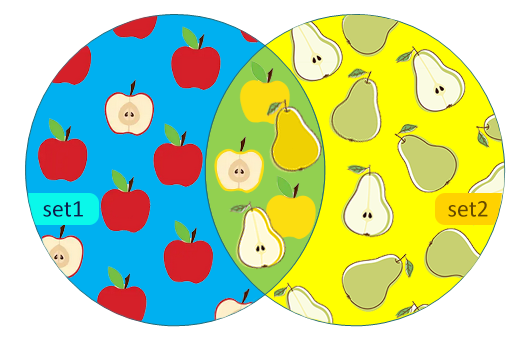
Рассмотрим два множества: красные яблоки и зелёные груши. При этом оба множества содержат жёлтые яблоки и груши:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}

Объединение двух множеств – это новое множество, которое содержит все элементы обоих множеств. В математике объединение двух множеств A и B обозначается как A ∪ B.

Для того, чтобы наглядно представить множества и отношения между ними, используем круги Эйлера. Каждый круг представляет одно множество, а область внутри него – его элементы. Перекрывающиеся области между кругами показывают элементы, которые являются общими для этих множеств.

На кругах Эйлера объединение двух множеств – это область, которая включает все элементы, принадлежащие хотя бы одному из этих множеств, то есть это общая закрашенная площадь всех кругов,

В Python найти объединение двух множеств позволяет метод set.intersection() и оператор |. Причём результаты как метода, так и оператора, полностью совпадают друг с другом.

Новое множество содержит как красные яблоки и зелёные груши, так и жёлтые яблоки и груши. То есть все элементы, присутствующие хотя бы в одном из множеств set1 или set2, но без повторений:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}
union_set = set1.union(set2)  # равносильно set1 | set2
print(union_set)
# Вывод: {'Жёлтые яблоки', 'Красные яблоки', 'Зелёные груши', 'Жёлтые груши'}

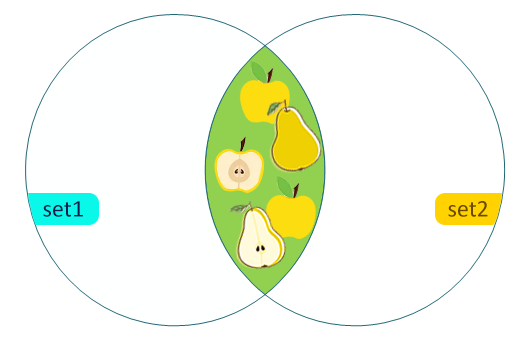
Пересечение двух множеств – это новое множество, которое содержит общие элементы обоих множеств. В математике пересечение двух множеств A и B обозначается как A ∩ B.

На кругах Эйлера пересечение множеств – это область, которая находится внутри пересекающихся кругов и представляет собой общие элементы, принадлежащие одновременно всем этим множествам.

Найти пересечение двух множеств позволяет метод set.intersection() и оператор &.

Новое множество содержит только жёлтые яблоки и груши, так как только они присутствуют одновременно в обоих множествах set1 и set2:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}
intersection_set = set1.intersection(set2)  # равносильно set1 & set2
print(intersection_set)  
# Вывод: {'Жёлтые груши', 'Жёлтые яблоки'}

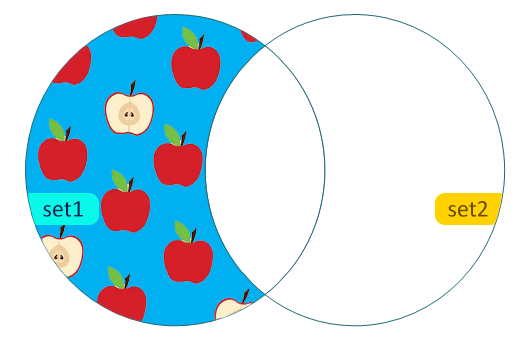
Разность двух множеств – это новое множество, которое содержит только те элементы первого множества, которых нет во втором. В математике разность двух множеств A и B обозначается как A \ B.

На кругах Эйлера разность множеств – это та часть круга первого множества, которая находится вне пересечения со вторым.

Найти разность двух множеств позволяет метод set.difference() и оператор -.

При вычислении разности множеств большое значение имеет порядок множеств. Так, если мы находим разность set1 - set2, то новое множество содержит только уникальные элементы множества set1, то есть красные яблоки, а если между set2 - set1, то уникальные элементы множества set2, то есть зелёные груши:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}
print(set1.difference(set2))  # равносильно set1 - set2
# Вывод: {'Красные яблоки'}
print(set2 – set1)  # равносильно set2.difference(set1)
# Вывод: {'Зелёные груши'}

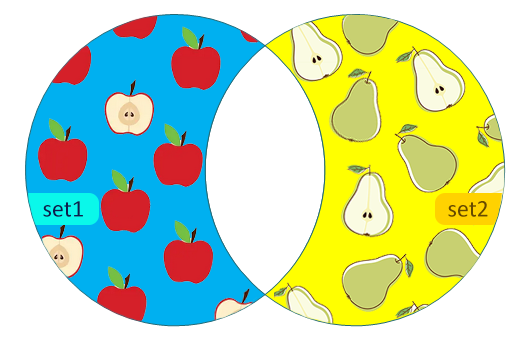
Симметричная разность двух множеств – это новое множество, которое не содержит общие элементы обоих множеств. В математике симметричная разность двух множеств A и B обозначается как A △ B.

На кругах Эйлера симметричная разность множеств – это область, которая включает в себя все элементы, принадлежащие только одному из множеств, и исключает общую пересекающуюся часть.

Найти симметричную разность двух множеств позволяет метод set.symmetric_difference() и оператор ^.

Новое множество содержит только красные яблоки и зелёные груши, так как исключаются все общие элементы множеств set1 и set2:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}
print(set1.symmetric_difference(set2))  # равносильно set1 ^ set2
# Вывод: {'Зелёные груши', 'Красные яблоки'}

Операторы с присваиванием для операций над множествами

Как и арифметические операторы, операторы для работы с множествами можно совмещать с оператором присваивания (=) и таким образом сразу присваивать новое значение переменной с исходным множеством:

set1 = {"Красные яблоки", "Жёлтые яблоки", "Жёлтые груши"}
set2 = {"Зелёные груши", "Жёлтые груши", "Жёлтые яблоки"}

set1 |= set2  # Объединение
print(set1)
# Вывод: {'Жёлтые яблоки', 'Красные яблоки', 'Зелёные груши', 'Жёлтые гру-ши'}

set1 &= set2  # Пересечение
print(set1)
# Вывод: {'Жёлтые груши', 'Жёлтые яблоки'}

set1 -= set2  # Разность
print(set1)
# Вывод: {'Красные яблоки'}

set1 ^= set2  # Симметричная разность
print(set1)
# Вывод: {'Зелёные груши', 'Красные яблоки'}

Во всех случаях исходное множество set1 перезаписывается новым множеством.

Сравнение множеств

Как числа и строки, множества поддерживают операцию сравнения, позволяя определять, является ли одно множество частью другого.

Например, у нас есть множество овощей, а также множество ингредиентов для овощного салата:

vegetables = {"Морковка", "Картошка"}
salad = {"Морковка", "Картошка", "Яйца", "Майонез", "Соль"}

Так как все элементы множества vegetables присутствуют в множестве salad, то множество vegetables является подмножеством множества salad, а множество salad – его надмножеством.

То есть подмножество – это множество, все элементы которого также принадлежат другому множеству, называемому надмножеством. Поэтому подмножество всегда меньше или равно надмножеству, а надмножество всегда больше или равно подмножеству. Это позволяет использовать уже знакомые нам операторы сравнения:

print(salad >= vegetables)
# Вывод: True

print(vegetables <= salad)
# Вывод: True

print(salad == vegetables)
# Вывод: False

print(vegetables != salad)
# Вывод: True

Операторам сравнения => и <= соответствуют свои методы:

• метод setissuperset(set2) соответствует оператору => (больше или равно) и проверяет содержит ли множество set1 множество set2;
• метод setissubset(set2) соответствует оператору <= (меньше или равно) проверяет является ли множество set1 частью множества set2.

Результат использования этих методов совпадает с результатом использования операторов сравнения:

vegetables = {"Морковка", "Картошка"}
salad = {"Морковка", "Картошка", "Яйца", "Майонез", "Соль"}
print(salad.issuperset(vegetables))
# Вывод: True
print(vegetables.issubset(salad))
# Вывод: True

Множества можно не только сравнить, но и проверить наличие общих элементов. Для этого предназначен метод set.isdisjoint().

Метод set.isdisjoint() возвращает True, только если они не имеют общих элементов:

vegetables = {"Морковка", "Картошка"}
fruits = ["Ананас", "Банан", "Дыня"]
print(vegetables.isdisjoint(fruits))
# Вывод: True
# Преобразуем во множество для операций над множествами
fruits_set = set(fruits)  
common_set = vegetables.intersection(fruits)
print(common_set)
# Вывод: set() <-- пустое множество

Результат этого метода необязательно совпадает с результатом проверки на неравенство (!=). Так как даже если множества не равны, то они всё равно могут иметь общие элементы:

salad = {"Яблоко", "Морковка"}
vegetables = {"Морковка", "Картошка"}
print(salad.isdisjoint(vegetables))
# Вывод: False
print(salad != vegetables)
# Вывод: True

Примеры

Пример 1. Полный список пользователей

Пользователи системы управления магазином могут иметь доступ к панели администратора, базе данных или к ним обеим одновременно. Программа объединяет множества пользователей обоих ресурсов и возвращает полный список уникальных пользователей:

# Пользователи, имеющие доступ к панели администратора
admin_users = {"nicholas_romanov", "boris_godunov", "yuri_zvenigorod", "support"}

# Пользователи, имеющие доступ к базе данных
db_users = {"boris_godunov", "dmitry_anuchin", "yuri_zvenigorod", "service_bot"}

# Все уникальные пользователи (объединение множеств)
all_unique_users = admin_users | db_users  # Эквивалентно: admin_users.union(db_users)

print(f"Пользователи с доступом к панели администратора: {admin_users}")
print(f"Пользователи с доступом к базе данных: {db_users}")
print(f"Все уникальные пользователи: {all_unique_users}")

Вывод:

Пользователи с доступом к панели администратора: {'nicholas_romanov', 'boris_godunov', 'yuri_zvenigorod', 'support'}
Пользователи с доступом к базе данных: {'boris_godunov', 'yuri_zvenigorod', 'dmitry_anuchin', 'service_bot'}
Все уникальные пользователи: {'nicholas_romanov', 'boris_godunov', 'yuri_zvenigorod', 'service_bot', 'dmitry_anuchin', 'support'}

Пример 2. Анализ поведения пользователей

В интернет-магазине в процессе анализа поведения клиентов сравнивают наиболее частые действия новых и постоянных клиентов:

new_users_actions = {"Поиск", "Просмотр", "Добавление в корзину"}
loyal_users_actions = {"Просмотр", "Покупка", "Отзыв"}

# Какие действия уникальны для новых клиентов? (разность множеств)
unique_to_new = new_users_actions - loyal_users_actions
print(f"Уникальные действия новых клиентов: {unique_to_new}")

# Какие действия совершают только постоянные клиенты? (разность множеств)
unique_to_loyal = loyal_users_actions - new_users_actions
print(f"Уникальные действия постоянных клиентов: {unique_to_loyal}")

# Какие общие паттерны поведения? (пересечение множеств)
common_actions = new_users_actions & loyal_users_actions
print(f"Общие действия: {common_actions}")

Вывод:

Уникальные действия новых клиентов: {'Добавление в корзину', 'Поиск'}
Уникальные действия постоянных клиентов: {'Покупка', 'Отзыв'}
Общие действия: {'Просмотр'}

Пример 3. Проверка выбора фильтров

Онлайн-платформа объявлений о продаже и аренде недвижимости требует обязательный выбор нескольких фильтров:

required_subcategories = {"Тип объекта", "Комнатность"}
user_input = {"Комнатность", "Цена", "Площадь"}

# Все ли обязательные фильтры присутствуют?
is_valid = user_input.issuperset(required_subcategories)
print(f"Указаны все обязательные фильтры: {is_valid}")

# Какие категории отсутствуют?
missing = required_subcategories - user_input
print(f"Отсутствуют фильтры: {missing if not is_valid else "нет"}")

Вывод:

Указаны все обязательные фильтры: False
Отсутствуют фильтры: {'Тип объекта'}

Итоги

Задания для самопроверки

1. Почему порядок множеств не имеет значения при их объединении, пересечении и симметричной разности, но критически важен при разности?

2. Объясните ключевое различие между операцией разности (-) и операцией симметричной разности (^) с точки зрения элементов, которые попадают в итоговое множество.

3. Даны множества set_a = {1, 2, 3, 4, 5} и set_b = {4, 5, 6, 7, 8}. Найдите и выведите на экран объединение, пересечение и симметричную разность этих множеств.

set_a = {1, 2, 3, 4, 5}
set_b = {4, 5, 6, 7, 8}
print(set_a | set_b)
# Вывод: {1, 2, 3, 4, 5, 6, 7, 8}
print(set_a & set_b)
# Вывод: {4, 5}
print(set_a - set_b)
# Вывод: {1, 2, 3}
print(set_a ^ set_b)
# Вывод: {1, 2, 3, 6, 7, 8}

4. Даны множества team_a = {"Иван", "Дмитрий", "Елена", "Ольга"} и team_b = {"Ольга", "Пётр", "Дмитрий", "Мария"}. Создайте и выведите на экран новое множество из участников, состоящих только в одной команде, а не в обеих.

team_a = {"Иван", "Дмитрий", "Елена", "Ольга"} 
team_b = {"Ольга", "Пётр", "Дмитрий", "Мария"}
team = team_a & team_b
print(team)
# Вывод: {'Дмитрий', 'Ольга'}

5. Даны множества colors1 = {"Красный", "Синий", "Желтый"} и colors2 = {"Синий", "Желтый"}. Проверьте, является ли colors1 надмножеством colors2, и является ли colors1 подмножеством colors2. Выведите оба результата на экран.

colors1 = {"Красный", "Синий", "Желтый"}
colors2 = {"Синий", "Желтый"}
print(colors1 >= colors2)
# Вывод: True
print(colors1 <= colors2)
# Вывод: False