Рекурсивные функции

Рекурсия – это способ решения задачи, при котором функция вызывает сама себя, и такая функция называется рекурсивной.

Рекурсия позволяет, не используя цикл, разбить задачу на более мелкие, идентичные части и решать каждую из них с помощью того же самого алгоритма. Это похоже на ситуацию, когда для выполнения задания часть работы передаётся тому же исполнителю, но в более простом виде.

Рекурсия состоит из двух ключевых компонентов:

• Базовый случай – это условие, при котором функция прекращает вызывать саму себя. Он является точкой выхода и предотвращает бесконечные вызовы.
• Рекурсивный случай – это часть, где функция вызывает саму себя, но с измененными аргументами, чтобы каждый следующий вызов приближал функцию к базовому случаю.

Факториал как рекурсивная функция

Факториал – это математическая функция, которая для числа возвращает произведение всех целых чисел от 1 до этого числа n включительно. Она обозначается восклицательным знаком после числа n и читается как n! (эн факториал).

Например, факториал числа 4 вычисляется как 4! = 1 * 2 * 3 * 4

Формально факториал для любого целого неотрицательного числа можно записать как n! = (n - 1) * ( − 2) * ... * 2 * 1.

При этом факториалы чисел 1 и 0 принято считать равным 1.

Факториал часто используют в комбинаторике и теории вероятности для подсчёта количества возможных перестановок. Однако нас больше интересует то, что вычисление факториала числа n – это классический пример рекурсивной функции.

Если мы запишем выражение для факториала как n! = (n - 1)!, то увидим, что определение факториала n! содержит в себе вызов самого себя (n - 1)! – это идеальный случай для рекурсии:

def factorial(n: int): -> int
    # Базовый случай: если n равно 0 или 1, возвращаем 1 и прекращаем рекурсию
    if n == 0 or n == 1:
        return 1
    # Рекурсивный случай: n! = n * (n - 1)!
    return n * factorial(n - 1)
    

print(f"5! = {factorial(5)}")
# Вывод: 5! = 120

Когда мы вызываем factorial(5), происходит следующая последовательность вызовов:

1. factorial(5) вызывает factorial(4);
2. factorial(4) вызывает factorial(3);
3. factorial(3) вызывает factorial(2);
4. factorial(2) вызывает factorial(1);
5. factorial(1) достигает базового случая и возвращает в factorial(2) число 1.

Каждая функция возвращает выражение n * factorial(n - 1). Затем вызовы начинают собираться в обратном порядке, вычисляя результат:

1. factorial(2) возвращает в factorial(3) число 2, как результат 2 * 1;
2. factorial(3) возвращает в factorial(4) число 6, как результат 3 * 2;
3. factorial(4) возвращает в factorial(5) число 24, как результат 4 * 6;
4. factorial(5) возвращает число 120, как результат 5 * 24.

Преимущество рекурсивных функций заключается в простоте их определения и ясной логике. Теоретически все рекурсивные функции можно записать в виде циклов, но логика циклов может быть не так ясна, как логика рекурсии.

Переполнение стека и максимальная глубина рекурсии

При использовании рекурсивных функций необходимо соблюдать осторожность, чтобы не допустить переполнения стека вызовов. Это происходит, когда функция вызывает саму себя слишком много раз, не достигая базового случая, что приводит к исчерпанию доступного размера стека вызовов.

Стек вызовов представляет собой специальную область памяти, которую операционная система использует для управления выполнением функций. Каждый раз, когда вызывается функция, Python создает для неё в стеке кадр стека, который содержит всю необходимую информацию: значения аргументов, локальные переменные и адрес, куда нужно вернуться после завершения работы функции.

Когда функция вызывает другую функцию, новый кадр вызова добавляется на вершину стека, и удаляется только после того, как функция завершила работу. Этот процесс работает по принципу, о котором мы упоминали, когда говорили о методе dict.pop() – «Последний пришел – первый вышел» или LIFO (от англ. Last In, First Out).

При использовании рекурсии каждый новый рекурсивный вызов добавляет новый кадр в стек. Если рекурсия не имеет правильно определённого базового случая или если он никогда не достигается, функция будет вызывать саму себя до тех пор, пока стек вызовов не заполнится.

Максимальное количество вложенных вызовов рекурсивной функции называется максимальной глубиной рекурсии и в Python по умолчанию составляет около 1000 вызовов. Когда размер стека превышает его, Python принудительно прерывает выполнение программы и вызывает ошибку RecursionError. Это и есть переполнение стека.

Вы можете столкнуться с этим, если попробуете вычислить факториал 1000:

print(f"1000! = {factorial(1000)}")
# Ошибка: RecursionError: maximum recursion depth exceeded

Однако факториал 999 должен быть вычислен:

print(f"999! = {factorial(999)}")
# Вывод: 999! = 40238726007... (очень большое число)

В большинстве случаев, если можно использовать простой цикл, лучше выбрать его. Рекурсию стоит применять, когда она делает код более читабельным и логически отражает структуру решаемой задачи.

Примеры

Пример 1. Ханойская башня

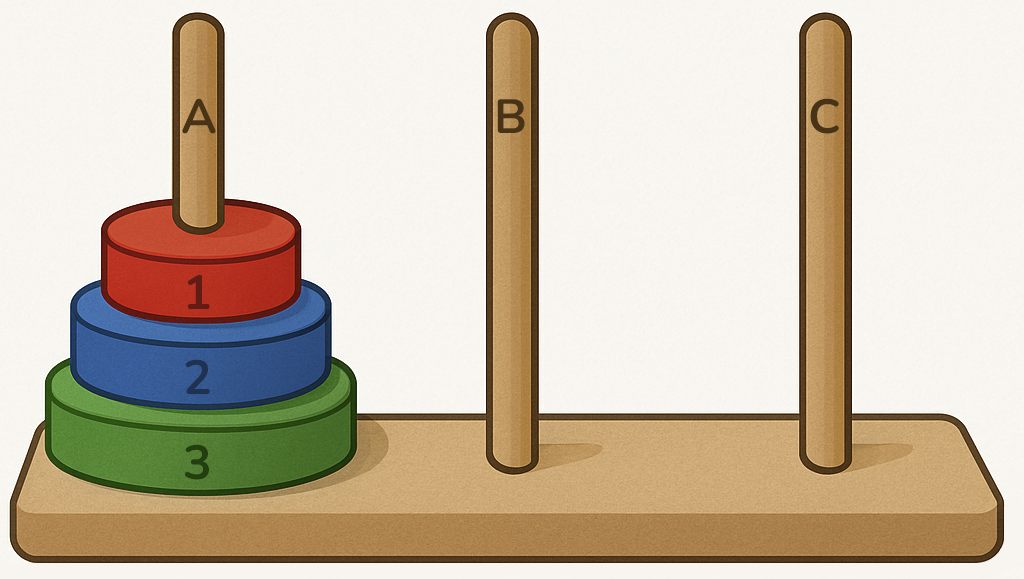
Ханойская башня – это популярная головоломка в виде трёх стержней, на один из которых надеты диски от большего к меньшему диаметру. Задача головоломки состоит в том, чтобы переместить все диски с одного стержня на другой за наименьшее число ходов. При этом необходимо соблюдать следующие правила:

• За один ход можно переместить только один диск.
• Диск можно класть только на больший диск или на пустой стержень.
• Нельзя класть больший диск на меньший.

Эту задачу удобно решить рекурсивно, так как её можно разбить на повторяющиеся однотипные подзадачи. Для того, чтобы перенести дисков с первого стержня A на третий стержень C, нужно выполнить три действия:

1. Переместить n - 1 дисков со стержня A на стержень B.
2. Переместить диск n со стержня A на стержень C.
3. Переместить n - 1 дисков со стержня B на стержень C.

При этом, чтобы переместить n - 1 дисков с первого стержня A на третий стержень B, нужно выполнить те же самые действия для n - 2 дисков. А для перемещения n - 2 дисков должны быть выполнены те же действия для n - 3 дисков и так далее.

Когда остался всего 1 диск, то есть n = 1, наступает базовый случай. Мы просто перекладываем этот диск со стержня A на стержень C, и рекурсия прекращается:

def hanoi(n: int, source: str, target: str, auxiliary: str) -> None:
    """Рекурсивно решает головоломку "Ханойская башня".
    
    Параметры:
        n: Количество дисков, которые нужно переложить.
        source: Стержень, с которого диски перекладываются.
        target: Стержень, на который диски перекладываются.
        auxiliary: Вспомогательный стержень.

    """
    # Если остался один диск (n = 1), просто перемещаем его
    if n == 1:
        print(f"Переместить диск 1 с {source} на {target}")
        return

    # Перекладываем n-1 дисков со стержня A на стержень B
    hanoi(n - 1, source, auxiliary, target)
    
    # Перекладываем оставшийся n-ый диск со стержня A на стержень C
    print(f"Переместить диск {n} с {source} на {target}")
    
    # Перекладываем n-1 дисков со стержня B на стержень C
    hanoi(n - 1, auxiliary, target, source)


hanoi(3, "A", "C", "B")

Здесь функция hanoi() вызывается для варианта головоломки, представленного на рисунке, то есть для трёх дисков и башен A, B и C.

Вывод:

Переместить диск 1 с A на C
Переместить диск 2 с A на B
Переместить диск 1 с C на B
Переместить диск 3 с A на C
Переместить диск 1 с B на A
Переместить диск 2 с B на C
Переместить диск 1 с A на C

Пример 2. Поиск наибольшего общего делителя

Наибольший общий делитель (НОД) – это наибольшее натуральное число, на которое два или более данных натуральных числа делятся без остатка. Например, для чисел 12 и 18 НОД равен 6, поскольку это самое большое число, на которое делятся и 12 (12 = 6 2), и 18 (18 = 6 3).

Наиболее эффективным способом нахождения НОД двух чисел является алгоритм Евклида. Он основан на том, что НОД двух чисел не изменится, если большее число заменить на остаток от деления большего на меньшее, то есть НОД(a, b) = НОД(b, a % b). Рекурсивная функция вызывает саму себя с обновленными значениями b и a % b, пока b не станет равным нулю, тогда наступает базовый случай, и функция возвращает a как НОД:

def gcd(a: int, b: int) -> int:
    """Рекурсивно находит наибольший общий делитель двух чисел
    используя алгоритм Евклида.
    
    Параметры:
        a: Первое число.
        b: Второе число.
        
    Возвращает:
        Наибольший общий делитель (НОД) чисел a и b.
    """
    # Базовый случай
    if b == 0:
        return a
    # Рекурсивный случай
    else:
        return gcd(b, a % b)


print(f"НОД чисел 48 и 18: {gcd(48, 18)}")
print(f"НОД чисел 270 и 192: {gcd(270, 192)}")

Покажем, как вычислялся НОД чисел 48 и 18:

• НОД(48, 18) – так как 18 не равно 0, вычисляем остаток от деления 48 на 18: 48 = 2 ⋅ 18 + 12.

Вызываем НОД(18, 12).

• НОД(18, 12) – так как 12 не равно 0, вычисляем остаток от деления 18 на 12: 18=1 ⋅ 12 + 6.

Вызываем НОД(12, 6).

• НОД(12, 6) – так как 6 не равно 0, вычисляем остаток от деления 12 на 6: 12 = 2 ⋅ 6 + 0.

Вызываем НОД(6, 0).

• НОД(6, 0) – достигнут базовый случай. Второе число равно 0, поэтому НОД – это первое число, то есть 6.

Вывод:

НОД чисел 48 и 18: 6
НОД чисел 270 и 192: 6

Итоги

• Рекурсивная функция – это функция, которая вызывает саму себя.
• Рекурсия состоит из базового случая – условия, при котором функция завершает вызывать себя, и рекурсивного случая – условия, когда функция вызывает саму себя для решения меньшей подзадачи.
• Факториал – это математическая функция, которая для числа возвращает произведение всех целых чисел от 1 до этого числа включительно. Это классический пример рекурсивной функции.
• Стек вызовов – это специальная область памяти, которую операционная система использует для управления выполнением функций.
• Кадр стека – это блок данных, содержащий информацию о функции: значения аргументов, локальные переменные и адрес, куда нужно вернуться после завершения работы функции.
• Работа рекурсивных функций опирается на стек вызовов, который работает по принципу LIFO или «Последний пришел – первый вышел». Когда функция вызывает другую функцию, новый кадр вызова добавляется на вершину стека, и удаляется только после того, как функция завершила работу.
• Максимальная глубина рекурсии – это максимальное количество вложенных вызовов рекурсивной функции (около 1000 по умолчанию).
• Ханойская башня – это головоломка в виде трёх стержней, на один из которых надеты диски от большего к меньшему диаметру. Её цель состоит в том, чтобы переместить все диски с одного стержня на другой за наименьшее число ходов. Это ещё один классический пример задачи на рекурсию.

Задания для самопроверки

1. Что такое рекурсия? Из каких двух ключевых компонентов она состоит?

2. Объясните, почему для рекурсивной функции необходим базовый случай. Что произойдёт, если его не будет?

3. Когда выполнение рекурсивной функции может привести к исключению RecursionError?

4. Что будет выведено на экран в результате выполнения следующего кода? Объясните свой ответ.

def mystery(n: int) -> int:
    if n == 0:
        return 1
    else:
        return 2 * mystery(n - 1)


print(mystery(3))

5. Напишите функцию power(base, exponent), которая принимает число base и целое неотрицательное число exponent, и возвращает результат возведения числа base в степень exponent. Используйте рекурсию, а не оператор **. Вызовите эту функцию для base = 2 и exponent = 4, и выведите результат на экран.

def power(base: float, exponent: int) -> float:
    # Базовый случай: любое число в степени 0 равно 1
    if exponent == 0:
        return 1
    # Рекурсивный шаг: base ** exponent = base * base ** (exponent - 1)
    else:
        return base * power(base, exponent - 1)


print(power(2, 4))